
Equation 6
The Redshift-Distance Equation.
We can readily observe Gravitational Redshift, for example light climbing out of the sun has all its wavelengths slightly shifted towards the lower energy ‘red’ end of the spectrum by the time it reaches us. For heavier stars, the effect becomes more pronounced. The gravity of the sun exists as a spacetime curvature which appears as an acceleration (a deceleration for anything trying to get away from it), this deceleration removes energy from light and causes a redshift.
Light traveling long distances across the universe becomes subject to its overall small positive spacetime curvature that also acts as a deceleration. This gives rise to a cosmological gravitational redshift in proportion to the distance travelled.
We calibrate redshift Z in terms of observed frequency over expected frequency and then subtracting one, so that the scale begins at zero rather than one.
Local galaxies have negligible cosmological redshifts. A redshift of Z = 1 corresponds to exactly half antipode distance. Light from near antipode distances has redshifts in excess of 10. Light from a luminous object at the antipode itself would have a redshift so high as to prevent its observation.
Counterfactual Indefiniteness.
Einstein famously asked if the Moon continues to exist when nobody looks at it.
I can now answer this with a (heavily qualified*) Not Necessarily.
An interesting example of this strangeness cropped up during some collaboration with a terrestrial correspondent upon Hypersphere Cosmology.
If cosmological redshift depends only on distance, then it has to remain indeterminate until measured.
See the graph below in which observed frequency (blue) decreases with distance travelled across the universe. This leads to an asymptotically increasing redshift of wavelength (red).
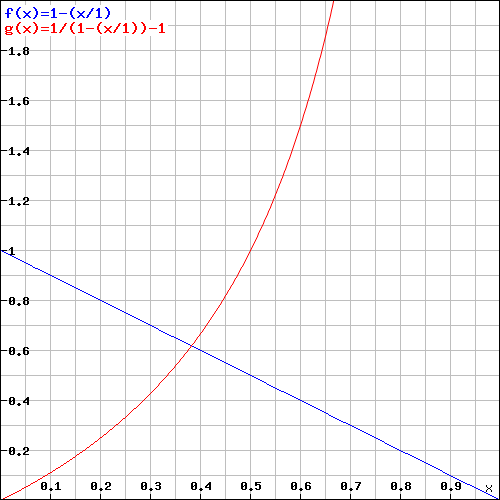
Note that as frequency decreases directly with distance travelled fo = fe (1-(d/L))
We cannot define what frequency a photon ‘would have’ at any point on a journey between two points, we can only calculate and confirm by measurement what frequency the photon has when we actually observe it. This means that the ‘counter-factual’ - the frequency that we do not observe, cannot have a definite but unknown value.
To take a simple example with rough figures: -
In Hypersphere Cosmology the antipode to any observer in the universe lies almost exactly 4 Gigaparsecs away, (1.23 E26 metres, 13 billion light years).
Imagine two distant galaxies ‘A’ at 2 Gigaparsecs, and ‘B’ at 1 Gigaparsec distant from an observer, with both laying roughly in the same direction. Light from A will have lost half of its frequency when it arrives at the observer. Light from B will have lost a quarter of its frequency when it arrives at the observer. This all accords with calculation and observation.
If we stopped the light from A at B, then we would find that it had lost a quarter of its frequency.
But what about the light from A as it flies unobserved past B? We cannot assign any value to its frequency that remains commensurate with the loss of a quarter of its frequency per Gigaparsec and a half of its frequency over 2 Gigaparsecs!
Plainly we have a quantum effect at play here. The frequency does not become defined until we stop the light and measure it, or equivalently it hits something and acquires a definite value.
Of all the interpretations of quantum mechanics, only Cramer’s Transactional Interpretation seems to offer a ‘reasonable’ or visualisable account of how this can happen. In this interpretation, retro causal advanced waves have to complete a quantum handshake across spacetime in any emission-absorption event before it acquires a definite value.
If, as in standard cosmology, the cosmological redshift arises from recession velocity in an expanding universe, then it can have a classical explanation that preserves the idea of a definite state of the unmeasured light at any point along its path.
Trans-Antipodal light and the CMBR
The sixth equation of Hypersphere Cosmology
https://www.specularium.org/component/k2/item/322-equation-6
shows how light become redshifted or frequency reduced as it travels across the universe by the universe’s small positive curvature which acts as an omnidirectional deceleration A.
It shows that light coming directly from the antipode point of any observer will lose all of its frequency and become unobservable: -
fo = fe (1-(d/L)) where fo = observed frequency, fe = expected frequency, d = astronomical distance and L= antipode distance.
However, due to the counter-factual indefiniteness of the frequency of a photon in flight, an observer can still receive photons from trans-antipodal sources so long as such photons undergo some form of interaction enroute, perhaps reflection or absorption and re-emission, in which case the mechanism works re-iteratively: -
fo = fe (1-(d1/L)) (1-(d2/L)) (1-(d3/L)) etc, where d1, d2, d3, etc, represent the distances travelled between interactions.
Clearly, if d1 + d2 + d3, etc > L then light can still reach an observer without its frequency reducing completely to zero.
The CMBR represents the light from incandescent hydrogen at around 3,000 Kelvin downshifted by a factor of about 1100 to just 2.7 Kelvin, and it comprises a dominant proportion of the photon count of the entire extra-galactic background light (EBL) spectrum.
Now assuming that starlight does ‘bounce around’ occasionally in the course of epic journeys including perhaps multiple trans-antipodal journeys, then we can perhaps expect ordinary starlight to reach thermodynamic equilibrium with the background temperature of the universe and supply the relatively intense Cosmic Microwave Background Radiation that we observe.