- Details
- Hits: 21800
Game of Thrones Risk Deluxe.
I enjoyed the Game of Thrones so much that I arranged to receive the board game for xmas. Okay, so it follows the usual Risk format which provides a reasonable ‘beer and pizza’ evening for 5 or 7 student age people if you play it straight. However the beauty of the map and the pieces led me to wonder if I could get more out of it by using it to tell a longer story as a one player game over a number of evenings, rather as one might enjoy reading or writing a novel within defined parameters.
Herewith my rough house rules: -
Setup on the Westeros board only.
Each house occupies all of its own territory, plus use the red pieces for the Iron Islanders.
Use the blue pieces for neutral territories (Vale of Arryn, Riverlands, Stormlands.)
Place the blue citadel on Kings Landing as a second Baratheon citadel.
Each territory generates 1 troop unit, as does each town and each port, citadels generate 3 units.
Each town and port and citadel generates 1 (100) gold.
Ships – I used the galleons out of ‘Civilisation’, you need about 10 ship markers. Each house starts with one, except the Iron Islanders who have 2. They begin and end turns in ports.
At each player turn, 1) adjust forces and income as above. 2) move any troops 1 space within occupied territory. Spend income if desired on fortifications, catapults, knights, reinforcements, or treachery.
Costs, fortifications, catapults, knights, ships, 3 gold each.
Treachery, to subvert an adjoining enemy unit pay 1 gold and throw a 2 or less on a D6, pay 2 gold and throw a 4 or less, or pay 3 gold and throw a 5 or less to change that unit to one of the active players own house. This only works at all if all units on a territory plus knights become subverted, otherwise it all fails, and the gold wasted.
Attack any neighbouring territories from ones you initially own. Ships carrying troops may attack up to 4 ports away, and may sail around the bottom of the map but not the top.
The usual rules of combat apply but with the following modifications, you can employ multiple knights and catapults, so towards the end of the game the 8 sided dice get used more. (you may need an extra 8 sided attack dice)
Citadels offer +2 to defenders on dice but only if the defenders elect to retreat to the citadel for a siege. Attackers can elect not to assault but to lay siege, in which case they own the territory, towns, and ports associated. If after 3 turns the siege remains in place, the defenders become eliminated.
Naval warfare. If a defender elects to defend an attacked port with ships then each ship can have a fighting crew of up to 3 troops plus up to 3 knights and one catapult if available, it may also carry another 3 troops as transports but not combatants. If a ship losses all three combat troops it becomes sunk, along with transports.
Ships can land troops on any territory to which a white line points even if it doesn’t count as a port, but then the ships must retire to their nearest friendly port.
Undefended ships in ports become automatically captured if attacked by crewed ships.
The single player should play each house in turn, considering the strategic options as they arise. Obviously alliances will become a critical consideration and part of the developing narrative. One simple rule can suffice here; any house breaking the terms of an alliance has to forgo all of its income in its next turn.
Objective- dominate Westeros, or at least form a stable alliance between the surviving houses.
Extra feature, when the last of the blue neutral pieces become eliminated the Undead as blue, begin to invade the The Gift. Roll a D8 to see how many appear each turn. They attempt to move south 1 territory per turn rolling D8s. Destroyed opposing pieces become replaced with undead pieces if they capture territory.
- Details
- Hits: 21812
Herewith a list of games that have particularly intrigued me over the years, some remain in print, some you can find easily on the net, others remain personal creations or in development. Games have made a considerable contribution to my thinking since an early age, not perhaps as much as books, yet interesting games function a bit like a books, and not only do they have a stories to tell in their structures but you can evolve stories as you play them or adapt them.
Careers. https://en.wikipedia.org/wiki/Careers_(board_game) I came across this at about age 12. I knew little about the world in those unsophisticated times and attended a grammar school where the English Master (a wily and provocative old cove) would occasionally announce ‘You are here to be educated as clerks, like your fathers’. Fortunately the school also had a science department, although nobody had a clue what you could do with a science education except become a science teacher. The school gave no career advice, it assumed you would either take one of the plentiful clerical jobs available at the time, or go to university and think of something whilst there. The game of Careers thus seemed an astonishing eye opener. Choose Wealth, Happiness, or Fame, join a whole series of professions, buy a yacht, in short; choose an Identity! All this seemed to sit in my subconscious till the mid-1970s, an era of plenty when career-anxiety seemed to give way to the search for personal identity in my peer group. I guess that I have always looked at life as a sort of board game. A lot of the assumptions built into the Careers game now seem simplistic but eventually it would perhaps have some influence over what I wrote in EPOCH, but more of that in a following article.
The Game of Nations. This came out in the 1970’s to model the then current oil crisis. Players control abstract Middle –Eastern oil producing territories and vie to get wealth that they can spend on oil extraction, tankers, and pipelines, or on taking over adjoining territories. The game system does not involve dice but it does have uncertainties built in with event cards. Players can buy Politicians, Secret Agents, Monarchs, Dictators, and Guerrillas in an attempt to subvert or conquer additional territories. Today we should perhaps consider adding Theocrats as well, and making the map less abstract and updating the events cards.
The Russians currently seem to play a strong hand in Syria. The West has perhaps made a mistake in supporting the ‘moderate’ rebels. Both sides need Iranian cooperation and support but if the Iranians come out of this on top then all hell may break loose if they go head to head with the Saudis.
Diplomacy. This classic game of early 20th Century European alliances represents one of the few games which model WW1 in an interesting way. Apart from the naval battle of Jutland the battles of WW1 mainly got settled by terrible attrition rather than by interesting tactics and manoeuvres. In Diplomacy we see the bigger picture as nations make secret alliances and agreements off board and then simultaneously reveal their strategies to see what results. Historians argue constantly about the causes of WW1, but in this model scenario, war seems virtually inevitable if the game represents the actual diplomatic system of the time. The game however does really need 5 or more players, but you can play it over many days with perhaps a move a day, and with secret diplomatic notes passed around at tea and lunch breaks.
Axis & Allies. The basic Axis & Allies game models WW2 from after it has started and Japan has attacked Hawaii and the Germans have attacked Russia. It can accommodate five players but it works well with just two. Basically it works a bit like the simple strategy game of ‘Risk!’ where you get extra forces for conquering more territory, however the forces consist of various types of land, sea, and air units which makes it far more detailed and engaging. Subsequent versions have striven for yet more detail and realism. The initial game suffered from the structural quirk that Japanese commanders with any sense should disengage quickly from the pacific and attack Russia in the east, thus virtually ensuring an Axis economic victory. However for historical reasons, notably the Nomonhan Incident, the Nazi-Soviet Non-Aggression Pact and an Oil Embargo, they adopted a Pacific strategy. The critical role of oil supply in WW2 does not seem well reflected in the basic rules.
Buck Rogers – Battle for the 25th Century. This quirky game never became very popular but you can get second-hand versions quite easily. It has an Axis and Allies type strategic structure but set in the inner solar system with spaceships and spacefaring troops disputing the control of Mercury, Venus, Earth, Mars, the Asteroids and various orbital facilities. It has the extraordinary feature of a variable geometry board. The Planets move around the Sun and you need to plan spacecraft trips accordingly. The basic game has some complications that I don’t find worthwhile; I have preferred to adapt the rules to make it more like Axis & Allies and also to use the Risk 2210 sci-fi pieces to provide more choices of troop type.
Discworld. Ankh-Morepork. Something extraordinary happened here and then a tragedy occurred. Perhaps by some happy chance a really good game got cobbled together in Ankh-Morepork, (two attempts to make sequels to it fell badly flat) but then after the death of Sir Terry Pratchett something went wrong with the rights and the publishers had to stop making it. Sets can now fetch several hundred pounds. The game has a bit of everything, it seems a bit like turbo-monopoly with assassination and magic, although amassing property may not necessarily win you the game because you don’t know which characters your opponents play. It works best with four players and it contains enough randomness and pageantry from the books to make it surprising and enjoyable for aficionados and beginners.
Space Raid. Interstellar board game design presents two major problems, firstly how to represent 3D space on a 2D board, and secondly how to allow for the vast distances and speeds involved. The designer needs to invoke or invent some reasonably credible but as yet undiscovered physics.
In designing Space Raid, I opted for sheets of black board with numbered or named stars on them joined by pale green lines representing possible jump routes between them of lengths of up to a few parsecs, to produce a sort of spider web or network of jump routes with the stars at the nodes and with most stars connected to between 2 and 4 others by jump routes. On the board the jump routes have different apparent lengths to represent the reality of the stars not all lying in exactly the same plane, but perhaps lying in the thickness of the plane of a spiral galaxy.

The starships move using (hypothetical) gravity focussing devices. By focussing the gravity drive exclusively on a nearby star, a ship accelerates towards it and achieve an immense velocity fairly quickly. It then performs a slingshot manoeuvre around the star and as it hurtles away it uses the gravity focussing drive to brake against the star to eventually bring itself more or less to rest around another nearby star. Thus each time a ship makes a jump it leaves one star system, hurtles through another without stopping, and ends up in a third. Two further quirks of relativistically dubious speculative physics also occur in this scenario, initiating a jump sends out a non-local gravitational hyperwake through the system so all ships know when another has jumped, but not to where, plus all jumps take a very similar amount of time, irrespective of differing distances.
Rather conveniently this leads to the situation where all ships on both sides can jump simultaneously but commanders don’t know the destinations of their opponent’s ships. So both sides secretly write down the next destinations of their ships and then both reveal them and move their ships and see if any have arrived at the same star systems, in which case combat begins. Plus ships passing through a star system in the middle part of their two star jump have such an enormous velocity that interception and combat remain impossible, however they can deploy kinetic energy weapons in passing, basically dropping rocks on very large targets like planets to create massive devastation. No defence exists against this except to intercept them well before they get within jump range of a star system with a base or colony on one of its planets. This does not seem unreasonable, the capacity for flight soon brought with it the capacity to wreck entire cities; the capacity of interstellar travel would probably bring with it the capacity to wreck entire planets. Players may agree to a treaty forbidding such tactics, or a severe loss of victory points if they break it.
When opposing starships end up in the same system they can attempt to engage or evade each other using a variety of sensors, cloaking devices, and evasive tactics, force shields, particle beam weapons, and missiles. Each ship has a variety of factors for these and duelling proceeds through the use of asymmetric combat polygons. Ships can also exchange fire with orbital bases or with planetary bases.
- Details
- Hits: 19847
Asymmetric Conflict Polygons
Uncertainty in games can come from either building in randomness with dice or shuffled cards or some other sortilege procedure; or from scenarios where players lack information about their opponent’s intentions.
Simultaneous Play often yields a system that models real life scenarios rather well. In this, the players secretly record their intended plays and then all reveal their orders and compare them to see what happens. The game of ‘Diplomacy’ which simulates the political alliances and military balances in Europe from 1900 onwards provides a classic example of a game based on simultaneous play with concealed intentions. Only rarely does peace prevail until 1914.
Some people find the use of dice or some other random mechanism unappealing as it can make the best laid plans come to nothing for no reason except bad luck, and it prevents any detailed analysis of a game afterwards.
The game of Scissors-Paper-Stone, sometimes called ‘Roshambo’, may well originate from the Han Dynasty era in China. It has attracted a considerable amount of study and competitive play, and computer algorithms exist against which humans can play. Although no strategy can consistently beat purely random play, competitions and algorithms remain interesting because few people can consistently play randomly and a good player or algorithm can anticipate the non-random choices of an opponent based on their previous choices.
Nevertheless the game remains rather trivial although the principle has become incorporated into some games to settle combats between pieces, for example in hand to hand conflict, Parry and Thrust beats Lunge, Lunge beats Slash, and Slash beats Parry and Thrust, or something like that. To a very simple approximation circa 1805, Artillery beats Infantry, Infantry beats Cavalry, and Cavalry beats Artillery.
Such a system of conflict resolution leads to a quick and easy type of duelling done with hand gestures, or with cards selected and put forward and then exposed. Yet in its simple form it seems little better than using dice. However by using something a little more sophisticated than a simple symmetrical triangle of outcomes we can create a facility for meaningful tactical choices with some uncertainty of outcome.
Consider the virtues of Asymmetric Conflict Polygons. An Hexagonal one appears below.
In this the six choices can represent any tactic from the exchange of fire between starships to the exchange of spells in a magical duel. The arrows between tactical choices show which choice wins and the weight of the arrow can show by how much. Each player in the duel has six cards marked with the tactical choices and both draw a card and then they simultaneously expose them and find the result. The asymmetries in the chart make some choices more favourable than others, depending on the powers of the pieces involved, however obviously the opponent will appreciate this.
The actual chart shown has the design feature that no choice offers guaranteed immunity from a full hit, but some choices offer greater chances of some kinds of hits.
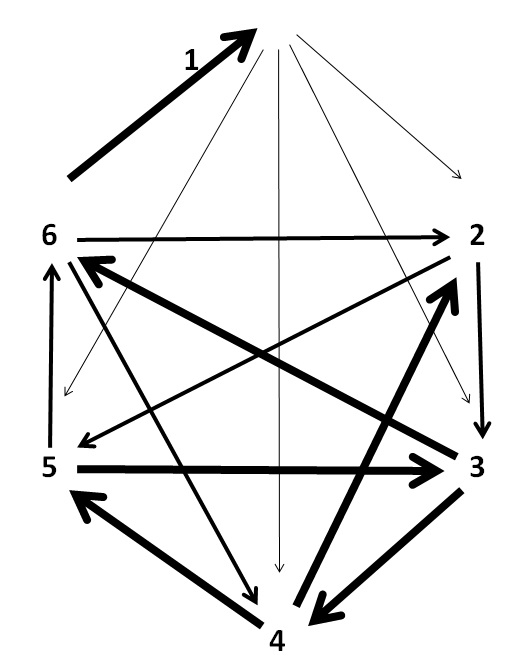
We could display the information on such a polygon with a simple 6 x 6 chart, however the polygon itself gives a much easier to use representation of the effect of one tactical choice upon another and the opportunities for second guessing the opponent.
Conflict polygons can also model the effects of offensive against defensive tactics where the attacker draws an attack tactic card and the defender draws a defensive tactic card.
In solo play an asymmetric polygon can allow the player to compete with intelligent choices against random choices generated by dice rolls.
- Details
- Hits: 21481
After decades of creating games of sometimes almost unplayable complexity the following game of Napoleonic Chess just sort of fell into place as part of a dice-free battle resolution system within a much larger strategic geo-political and economic game scenario. (I still work on that, particularly the naval aspects.)
However the game of Napoleonic Chess ™ has such an elegant simplicity and playability to it that I declare it Copyright Peter J Carroll 16/2/2016 ©.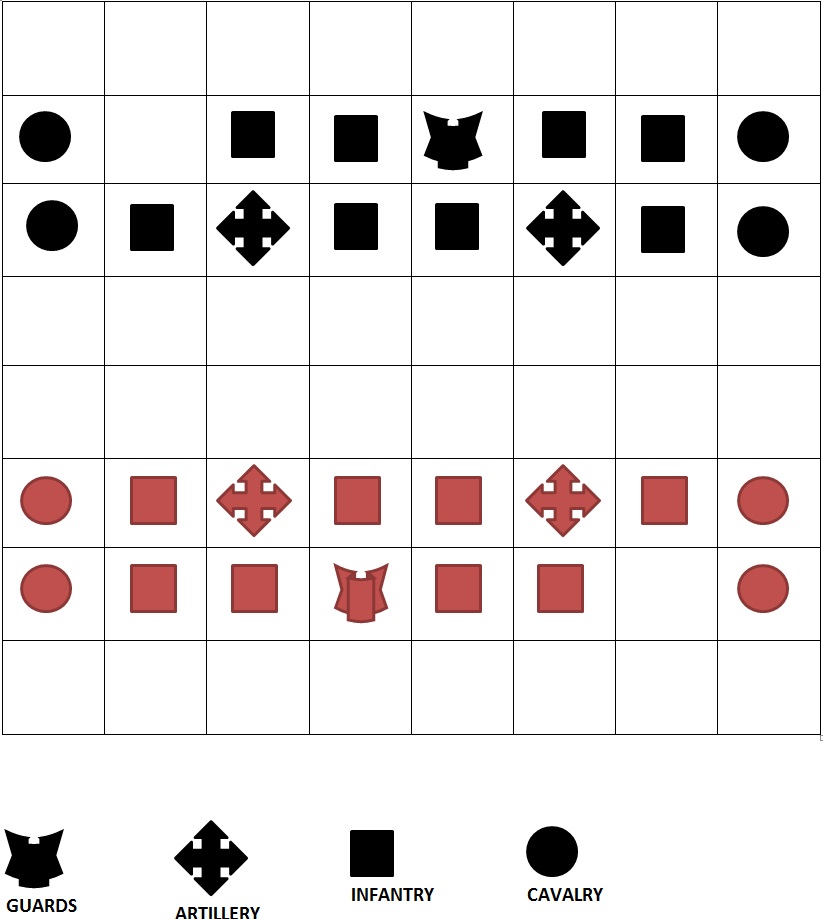
Napoleonic Chess.
A tactical game system for Napoleonic era battle simulation which players can use on an ordinary chess board using chess pieces, or extend to larger boards, add terrain features, or add additional units. This system differs radically from chess in that players may move all of their pieces in their turn.
The basic rules for the Standard Scenario appear below, followed by suggestions for more sophisticated scenarios.
Standard Scenario.
Players set up as shown with units on the 2nd and 3rd and the 6th and 7th rows. If using a standard chess set, discard the queens; use the pawns as infantry, knights and bishops as cavalry, rooks as artillery, and the king as guards. Alternatively for a better appearance and ease of use, take 2 chess sets and use all the knights for cavalry and both queens for artillery on each side. Alternatively acquire or make some period pieces.
Each side moves alternately and settles all resulting attacks, and each player may move all their units during a single turn.
Movement and Combat. Units basically move (or not) and then attack in a single turn.
Infantry may move a single square in any direction.
Infantry attacks or supports orthogonally only, with a value of 1, into an adjacent square. Infantry has a defensive value of 1.
Cavalry may move one or two squares in any direction.
Cavalry attacks or supports diagonally only, with a value of 1, into an adjacent square. Cavalry has a defensive value of 1.
Artillery may move a single square orthogonally only.
Artillery attacks orthogonally only with a value of 2, into an adjacent square.
Artillery supports into an adjacent orthogonal square with a value of 1.
Artillery has a defensive value of 1.
The Guards may move a single square in any direction.
Guards attack or support in any direction with a value of 1, into an adjacent square.
Guards have a defensive value of 2.
Any unit may make only a single attack or defensive support in a players turn, or a single defensive support against attack in an opponents turn.
Eliminating pieces.
Any unit coming under attack by attack values which exceed its defence value plus the value of any support it receives becomes eliminated and removed from the board.
One of the attacking units may then move straight on to the square it occupied if the attacker so wishes.
A unit under attack cannot offer support to an adjacent unit.
Victory Conditions. Elimination of the enemy Guard unit; or the enemy surrenders.
Example of a complex attack.
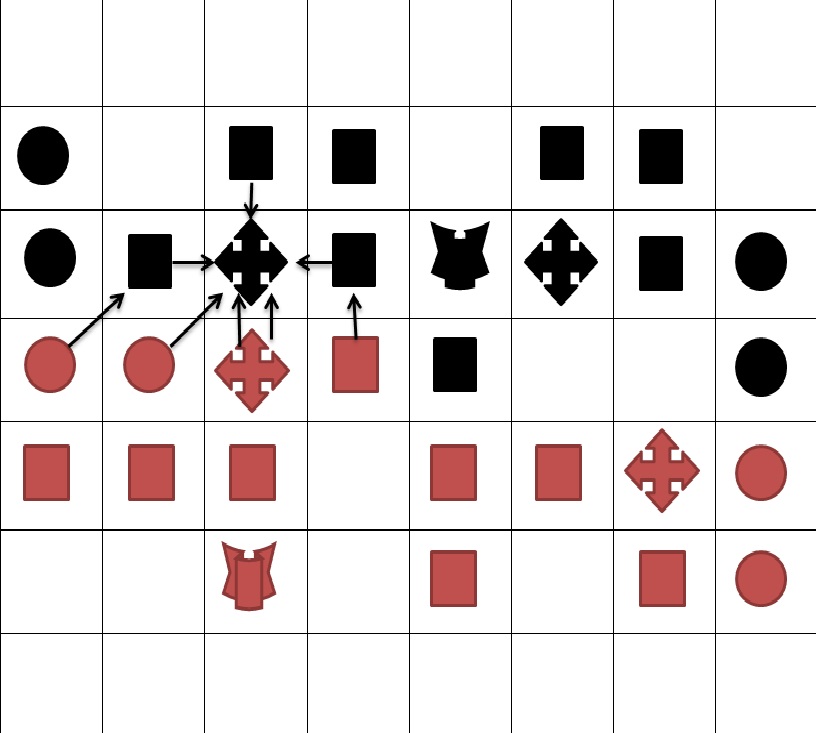
Here Red attacks the Black Artillery unit with Artillery. The 3 orthogonal Black infantry units support the Black Artillery but the support of the ones on either side becomes removed by attacks from Red Infantry and Red Cavalry, so it only has support from the Black Infantry behind so it has a total defence value of 2, whereas Red attacks it with an attack value of 3, one from the Red Cavalry and two from the Red Artillery, so it becomes eliminated. Red then has the option of immediately moving either the attacking Red Cavalry unit or the Red Artillery into the vacated space. (Although this would prove very risky).
Advanced Scenarios.
1) Alternative Standard Scenario Initial Dispositions.
a) Attack at Dawn. Both sides write down their desired positions of their units on the 2nd and 3rd and the 6th and 7th rows in secret and then reveal them and lay out their units.
b) Marching Orders. Players take it in turn to place one unit (or more if agreed) on the board at a time in the appropriate rows till all units have become deployed.
2) Additional/Variant Units.
Horse Artillery moves 2 squares in any direction.
Horse Artillery attacks and supports in any direction into adjacent squares with a value of 1.
Horse Artillery has a defensive value of 1.
Dragoons move two squares in any direction.
Dragoons attack and support into orthogonal squares only with a value of 1.
Dragoons have a defensive value of 1.
Foot Guards, as for Infantry but with a defensive value of 2.
Cuirassiers/Horse Guards, as for cavalry but with an attack value of 2.
3) Optional Terrain Features. (Made by placing an appropriate card tile on a square)
Hills – add one to the defensive value of a unit on a Hill square unless attacked from an adjacent hill square. Units cannot move on and off a Hill in a single turn.
Redoubts - (earthworks etc.) - these take an agreed number of turns of uninterrupted occupation of a square to construct, and then function as for Hills. Artillery attacking into a redoubt attacks at only 1, and cannot enter an enemy redoubt on the same turn if it falls.
Square Border Obstacles – watercourses, banks, ditches hedges etc. – These can mark one or more of the edges of a square. They give +1 defensive value if they protect a unit from all units attacking it. Artillery has only an attack value of 1 across such obstacles.
4) Larger Boards, Bigger Battles with More Units, Multiple Armies, Multiplayer, Divided Command and Strategic Scenarios.
This system will support all of the above. Allied units from different armies or command structures may support each other by attacks without moving, or by supporting in defence.
In Strategic Scenarios stretching over continents and using markers for entire armies, this system provides a means of resolving battles at a tactical level.
In larger battles it often helps to number the pieces to keep track of which have moved and which haven’t in a turn. 1st, 2nd and 3rd infantry etc.
Other Epochs. This battle system can support a variety of pre-gunpowder conflict scenarios by simply substituting Heavy Infantry for Artillery.
- Details
- Hits: 18901
Academic Games Theory concerns itself with decision making in abstract, theoretical or hypothetical situations in the hope of working out what decisions agents might or should take in the real world. As such it has attempted to model tactical and strategic behaviour in many fields from gambling and criminality to economics and warfare. Biologists have even tried adapting it to explaining hunting and mating strategies.
The famous Prisoners Dilemma in which two subjects have to choose between incriminating the other or keeping silent has many variants, but basically if both keep silent they both get a small sentence; by incriminating the other, either can go free but with the other getting a large sentence; however if both incriminate the other then they both get a fairly large sentence.
However this theoretical scenario does not easily model the real life behaviour of the police who invariably try to separate suspects and to heavily hint that their associates have already incriminated them, or the degree of honour or animosity between thieves.
The modelling of economic behaviour used to depend entirely on the ‘Rational Agent’ proposition that people will always act to maximise their monetary gain. However experiments tend to show that people have an irrational aversion to loss, regretting the loss of a small amount more than valuing the gain of a larger amount, and that they tend to suffer from the sunk costs fallacy and throw good money after bad, and that they generally conform to herd mentality, and that they frequently invest in Meaning rather than Utility. Yet even with such added sophistications ‘The Dismal Science’ of Economics still has very low predictive power.
Warfare, the game of kings, has invited theoretical modelling and representation since the earliest of times with the game of Chess and its oriental equivalents providing prime examples. However such semi-abstract games lack the complexities of real warfare and combative nations have never agreed to settle conflict by simulation, except perhaps for the nuclear standoff conflict where most simulations simply offered Mutually Assured Destruction or Not, and they chose Not.
Personally I hate straight Chess, it seems to require far more concentration than imagination and its very abstractness does not fire my imagination. There seems little point in playing except to win, and playing to win, particularly against computer programs, just gives me headaches for very little reward. Playing to win against friends tends to sour friendships. On the other hand some board wargames have an intrinsic pageantry or historical interest or imaginative component that makes the play itself interesting, win or lose.
I also hate Monopoly because of its complete lack of realism, you get money for nothing, go to jail for no reason, the rent and taxes come in randomly, you have no choice of movement, it doesn’t teach you anything about capitalism, it takes far too long, and play doesn’t improve much with practise because like most ‘family games’ it involves a great deal of chance.
Uncertainty and chance provide much of the fascination of games and perhaps the only rationale for war or perhaps for even living at all. Yet uncertainty comes in two forms, lack of information and randomness. Some philosophers and classical physicists will argue that randomness simply consists of our lack of sufficient information. Other philosophers and most quantum physicists will argue that randomness actually underlies the apparent order of the universe which doesn’t really have a deterministic future state. Either way for the purposes of argument here we shall regard fair dice as ‘fair’, i.e. random in their output.
The appeal of uncertainty seems to lie in the pleasure we get from resolving it which tends to arise as either as a feeling of surprise and discovery and/or of control or vindication.
The degrees of imaginative symbolism, chance, imperfect information, and decision making, seem to define the quality and appeal of any game.
Games of pure chance rarely have much intrinsic interest except for those deluded by various gamblers fallacies, those who know how to cheat, and those with the mathematical expertise and investment capital to offer gambling facilities.
Snakes and Ladders seems utterly tiresome and pointless, and a bizarrely misguided attempt to model moral principles (originally it had all the ladders labelled with moral virtues and all the snakes labelled with moral vices) because ‘players’ have no choices at all in this game of pure chance.
Perhaps Snakes and ladders has its ultimate origins in the Neoplatonism that spawned Gnosticism, Hermeticism, and Kabala in the first couple of centuries AD, for these have various emanations, archons, and sephiroth that the supplicant must ascend like some sort of ladder to heaven. The Kabbalistic Tree of Life in its later representations has a downward pointing sword of the cherubim and an upward climbing serpent of wisdom.
Some people have looked to games of chance as a means of divination, presumably on the basis of the hypothesis that two unknowns like the outcome of the game and the outcome of reality, should have correlations because they already have the correlation of both having uncertainty at the outset.
Chess on the other hand contains no element of chance; the uncertainty arises purely out of the lack of knowledge of one’s opponent’s detailed intentions. The power of a chess piece depends only on its movement and a weaker piece may take a strong piece as readily as an even stronger one can, plus players may only move one piece per turn, both of which render the game almost entirely abstracted from real conflict.
The best strategy games usually involve decisions and choices, and uncertainties arising from both concealed intentions and chance. In these, the role of chance usually kicks in at a fairly low grain size within the game to settle tactical outcomes that the game does not model in detail but it does so in a weighted fashion to reflect the probability of the outcome. If in Chess, pawns and kings threw 1 dice, knights and bishops threw 2, rooks and queens threw 3, and the highest score won each attempt to take another piece, you could convert it into a simple poor relation of a battle game with weighted chance. Alternatively the use of Polyhedral Dice as actual playing pieces with the more multi-faceted ones representing the more powerful pieces, works quite well.
‘Risk!’ the game of world conquest, appears as the grandfather of most popular multiplayer strategy games and it keeps getting released dressed in yet another historical or futuristic format almost yearly. I tend to buy these up just for the pieces these days as you can get a large Napoleonic, or Fantasy, or Science Fiction army of playing pieces very cheaply due to the continuing popularity of the fairly simple game system itself. This system depends on conquering territory to get more armies to conquer yet more, with a numbers weighted chance attrition system of conflict resolution. A semi-random system of bonus armies increases the uncertainties of the game, and some variants have concealed victory conditions for the players.
I grew up playing ‘Risk!’ with my school friends but later opted for the more sophisticated Avalon Hill and ‘Allies & Axis’ simulations of WW2 which incidentally stimulated a fair bit of detailed research into the history of WW2 for the eventual creation of a tournament version on a two square metre board with hundreds of pieces and almost real time play, well it took so long that few games ever got finished.
Through life I have tended to spend more time on the game of analysing and creating games than I have on actually playing them.
At about age 14 I sent a game I called ‘Space Race’ to Waddington’s; I distinctly remember the sheet of starry wall-paper used for the board. I got no reply but a couple of years later they brought out ‘Blast Off’ based on virtually identical principles, a race around the solar system with fuel as a critical resource. Apparently you have five times the chance of getting a book published than a game, I never bothered again.
A modified game of Cluedo to include Motive* and Time of Death also got made, how odd that a detective game should have omitted such things. (*The Seven Deadly Sins.)
There followed an attractive looking 3D chess board made out of four 4x4 Perspex sheets. Moves became almost impossibly complicated, particularly if diagonal moves could include movement through the vertices of the cubic cells. 4 Dimensional chess played on a 1+ 8x8x8x8x8x8 Perspex hypercube received some theoretical attention but never got built, with more than 3 or 4 pieces per side it would have become incalculably difficult in those pre-computer days.
Designing Space and Magical battles provided endless fascination, in the first case because it forces the designer to think about the undiscovered physics involved, and in the second case because it forces the designer to think about the alternative physics involved.
Thus the game of designing games can become a far from trivial pursuit. To model an existing or historical reality you first have to find out how it actually works or worked. To create a new reality you need to make it self-consistent and credible.
If reality consists of a game we play inside our heads then you need an accurate representation of existing reality and a credible and self-consistent model of any planned extension of it in your dreams.