Unlike the Hypersphere Cosmology model on this site which has achieved maturity and a fully quantitative exigesis, this investigation into the quantum microcosm remains speculative, experimental, qualitative, and a work in progress. All criticism and collaboration welcomed by email.
Descriptions and Explanations. Any Explanation of phenomena depends on Descriptions of underlying phenomena. Thus, for example, we explain chemistry in terms of atoms, and we explain atoms in terms of quantum physics. However, we have no satisfactory description of the phenomena underlying quantum physics yet. These musings experiment with descriptions of possible spacetime geometries underlying quanta and quantum fields. Any such description should explain the existence and behaviour of known particles and fields and if possible, make novel predictions.
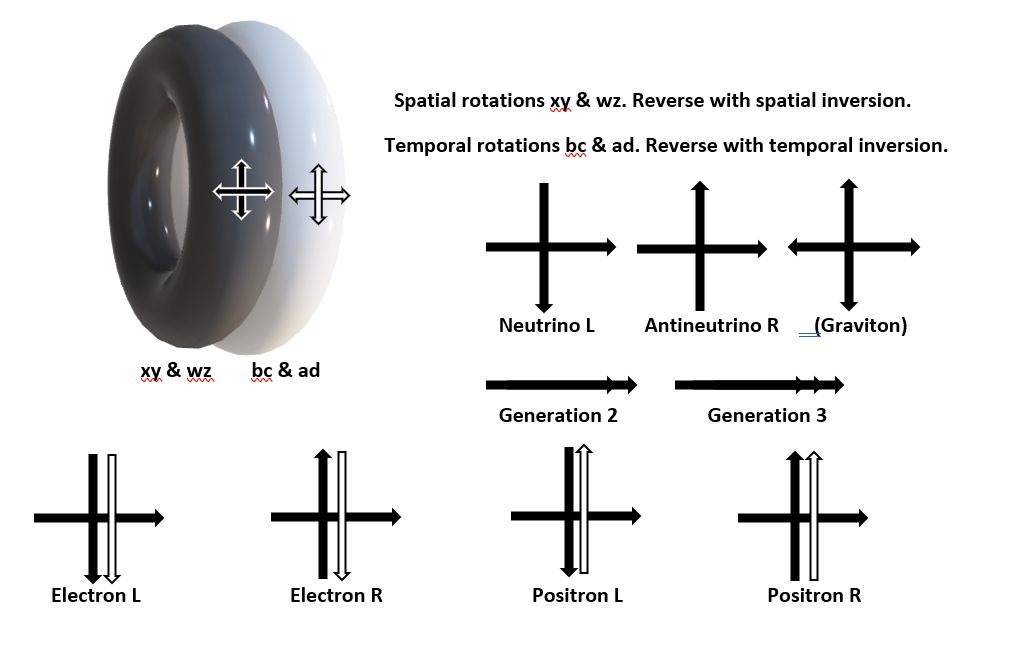
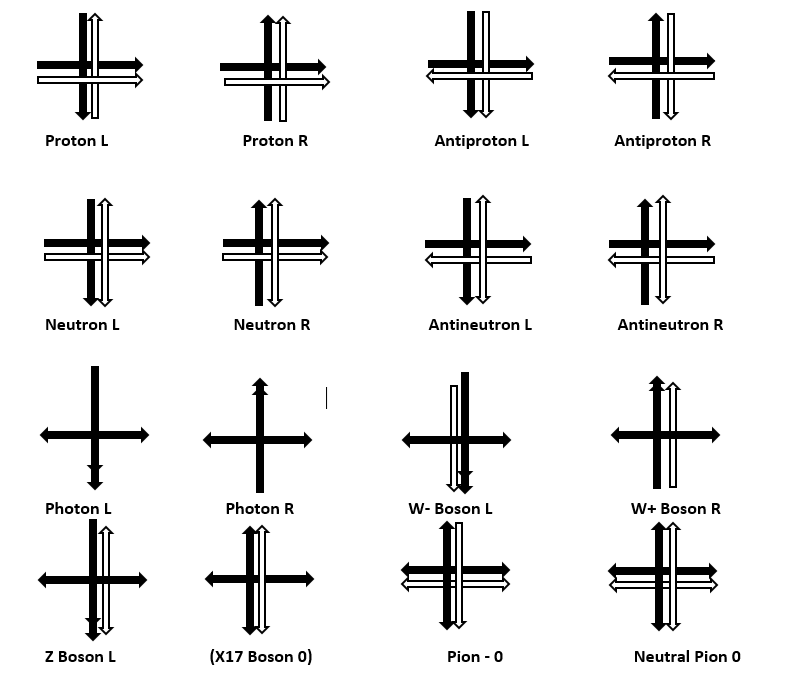
Table of fundamenal particles modelled as toruses.
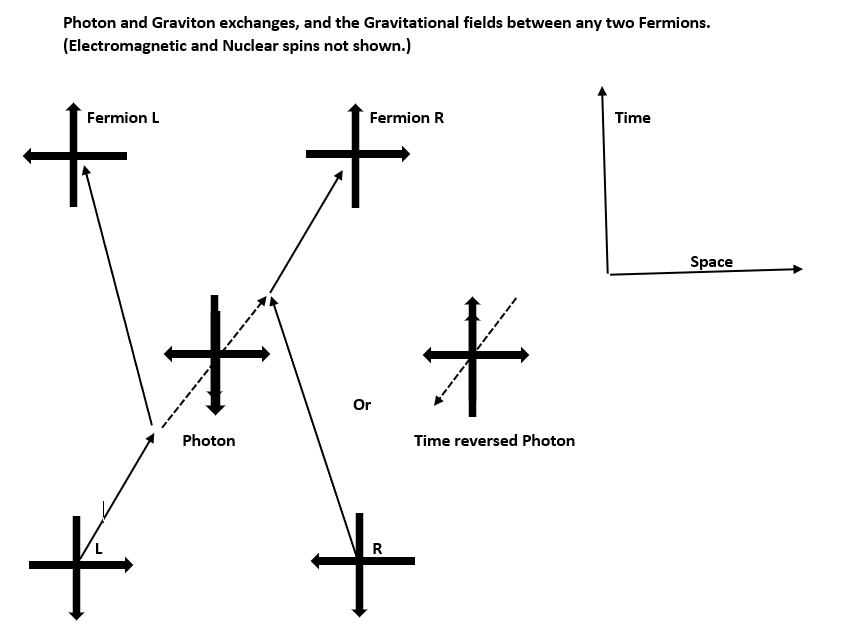
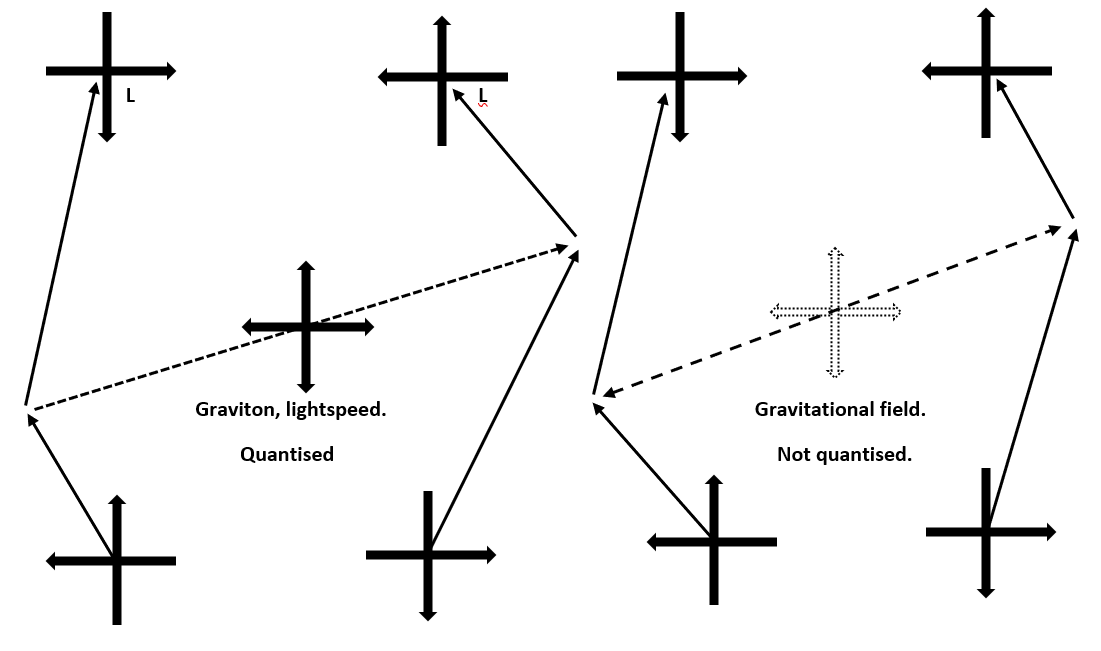
Table of simple partice interactions
This model begins with the simplest quantum, that of the neutrino, modelled as a spinor based on a Clifford Torus that rotates twice in the toroidal mode for each poloidal rotation.
This spinorial rotation allows for only two orientations of the poloidal rotation with respect to the direction of travel which lies orthogonal to it as neutrinos always travel at lightspeed. These two orientations correspond to neutrino (left) and antineutrino (right).
This spinorial rotation subtends a wavelike series of twists throughout all spacetime that extends across the universe and creates a field surrounding the particle.
Charged quanta result from rotations involving the pseudo-spatial plane of imaginary time, poloidal rotations give rise to positive and negative electric charges and toroidal rotations give rise to positive and negative nuclear charges. These also subtend wavelike series of twists throughout all spacetime that extends across the universe and create fields surrounding the quantum.
Quanta do not have a zero-dimensional point-like geometry, they consist of Clifford Tori with a similar topology to Hyperspheres (3-Spheres) except that they have a directionality of spins and propagation.
Quanta arise where incoming waves returning from the rest of the universe undergo a spinorial 3-Rotation and become outgoing waves. Spacetime consists of a single field which can carry several different types of twist or wave.
Electrostatic and Gravitational fields effectively act across any distance but with an effect that diminishes with the inverse square of distance. Fields rather than quantised particles mediate these interactions. Virtual non-quantised ‘particles’ do not exist, although images of them may prove useful in visualising the field geometry.
Photons consist of quanta of spins that become exchanged between fermions, these always propagate at lightspeed and always have a repulsive effect with both fermions recoiling. They do not carry electric charge and neither do electric fields affect them. We only regard them as the quanta of electromagnetism because we only observe their interactions between charge carrying fermions.
Gravitons appear as gravity waves when enormous masses accelerate, and they propagate at lightspeed with an exclusively attractive effect. Ordinary gravity works via fields.
Exchange particles such as photons and gravitons and all other bosons have a particle-antiparticle configuration, the exchange of such quanta occurs as a quantum handshake as in the Transactional Interpretation of Quantum Mechanics. Field effects arise in the same way although at the lower energies involved they do not give rise to quantised boson particles.
This model accommodates an additional charged boson to complement the W+, W-, and Z. This X17 boson has probably already appeared in the decay of Beryllium 8.
In this model all spins remain conserved on the basis that + and – equals 0, allowing for both particle creation and annihilation, energy permitting. Generation or ‘flavour’ remains conserved over a complete cycle of particle-antiparticle creation and subsequent decays.
The whole of QCD becomes discarded, gluons do not exist. Exotic transiently stable baryons and mesons simply have extra spins about the basic baryon or baryon-antibaryon configurations.
The mass-energy equivalence and the equivalence of inertial and gravitational mass arise from the effect of all the other spins upon the xy/wz spinors of quanta.

All particles extend fields right around the hypersphere of the universe, these converge at antiparticles at their antipodes. This explains the apparent lack of antimatter in the universe.
In/Out waves of spin converge and undergo 3-rotation to make non-point particles of finite size.
Every particle depends for its properties on the whole of the rest of the universe.
The Ubiquity Constant and the quantisation scale depend somehow on the macrostructure of the universe.
Quantised ‘kinks’ in space can only move at lightspeed, or less if they embody the temporal electric or nuclear spins which confer mass.
The Higgs mechanism does not apply. If the tiny 125 GeV blip corresponds to anything it probably corresponds to a transient ZZ di-boson.
Volume = 2pi2r3 for both a hypersphere and a (Clifford?) horn torus.
Does the local field geometry change from a vorticitating 3-Hypersphere to two rotating 3-Tori upon particle-antiparticle pair production and thus confer particle directionality?
Can Macrostructures modulate waves to carry structural information?
If so, all manner of psi effects and morphic field effects become possible and the universe will exhibit Stochastic Holism.
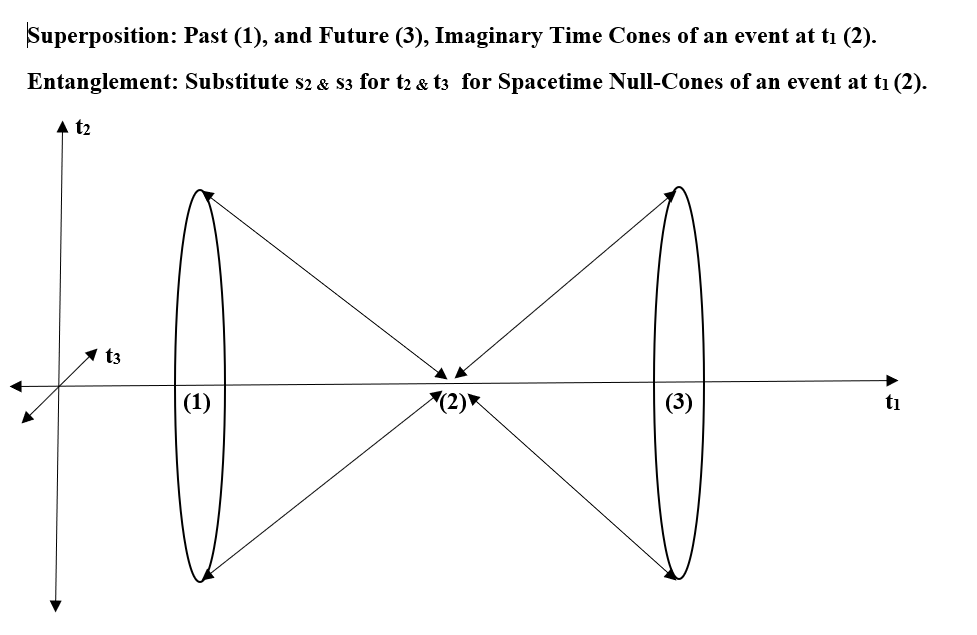
Three Dimensional Time Resources.
Herewith a selection of some of the main papers on 3D Time and SO(3,3) spacetime.
https://arxiv.org/pdf/quant-ph/0510010.pdf
https://phys.org/news/2007-04-mathematician-extra-dimensions-time-like.html
See also original paper, later published by the Royal Society.
https://arxiv.org/pdf/gr-qc/0610068.pdf
https://www.researchgate.net/publication/278410426_Could_time_be_three-dimensional
https://arxiv.org/pdf/quant-ph/0510010.pdf
http://cdsweb.cern.ch/record/688763/files/ext-2003-090.pdf
Herewith a fascinating piece of speculation from Gerard 't Hooft
https://arxiv.org/abs/2107.14191
https://arxiv.org/pdf/2107.14191.pdf
See the 'fast variables' and multidimensional toroids.