Unlike the Hypersphere Cosmology model on this site which has achieved maturity and a fully quantitative exigesis, this investigation into the quantum microcosm remains speculative, experimental, qualitative, and a work in progress. All criticism and collaboration welcomed by email.
HYPERSPHERE QUANTOLOGY
Many claim that any verbal or visual conceptions of quantum reality will always prove inadequate and that only highly abstract mathematical descriptions with no verbal or visualisable correlates will ever prove useful. That sounds like the very worst of quantum mysticism from the priesthood of science. Thou shalt not speak nor make graven images of the quanta!
What the heck, heresy always seems the best long term policy, so herewith the latest experimental musings upon Hypersphere Quantology, in the quest to demonstrate that magic arises as a natural property of the universe that conscious creatures can and do use.
Additional Ingredients: -rTIQM + WsM + HC + 3DT = Provisional Quantum Ontology.
https://www.npl.washington.edu/av/altvw16.html
(The (Relativistic) Transactional Interpretation of Quantum Mechanics (Cramer, Kastner) + The Wave Structure of Matter (Milo Wolff) + Hypersphere Cosmology +3DTime (Stokastikos).)
Presently the hypothesis exists as a generalised conceptual scheme expressed in terms of geometry and symbolic vector diagrams, perhaps the algebra may follow and then a reconciliation with observable numerical quantities.
The following diagrams represent Fermions, (matter ‘particles’) as Spinorial Rotations of spacetime. Such rotations in two directions at once allow a portion of spacetime to revolve with a 720 degree revolution restoring the ‘particle’ to its original position without tearing spacetime but sending a wavelike twist in all directions through it.
The longer black arrows represent the rotation of the particle with respect to its forward direction of propagation (at lightspeed). (Imagine the poloidal revolution of a Torus.) The shorter transverse black arrows represent spins orthogonal to the forward propagation. (Imagine the toroidal revolution of a Torus.) These diagrams show only one such transverse arrow for clarity – but various transverse arrows can represent chiral spin, or the higher dimensional spins associated with electromagnetic, nuclear, and generational charges.
The grey arrows represent the Advanced (backwards in time) waves used in the Transactional Interpretation of quantum mechanics, (so the black arrows represent the Retarded (forward in time) waves). The Transactional Interpretation alone seems the only interpretation capable of explaining the phenomenon of Entanglement and apparent Superposition. It also accounts for the seemingly instantaneous ‘effects’ of static fields.
Bosons appear in the diagrams as Retarded/Advanced wave pairs or equivalently as Particle/Antiparticle pairs, or the outward and inward waves of WSM. At low energies such Bosons remain ‘virtual’ and communicate only repulsive forces between Fermions (matter particles). At higher energies Bosons can become ‘real’ and transfer spin based charges such as chirality and electromagnetic, nuclear, and generational charge.

Diagram 1 shows an idealised Fermion as the origin of spherical waves that propagate to the antipode of the hyperspherical universe and then reconverge back there as suggested here: -
https://wsminfo.org/articles/GREIT6Oct06.htm
However this idea makes much more sense in terms of retarded and advanced waves (as in TIQM) going to, and coming back from, the antipode position of the fermion in a hyperspherical universe (finite and unbounded in both space and time) which naturally inverts the spatial and temporal spins of anything traveling right across it.
The outward/inward, retarded/advanced, particle/antiparticle spin zero boson remains virtual and hence acts as a field – in the simplest case the gravitational field which may slightly reduce the amount of spacetime between particles, causing a tension.

Diagram 2 shows how a virtual or real boson exchange between two fermions can give rise to a repulsive effect. At low energies the boson remains virtual, giving rise to a simple repulsive force. At higher energies the exchange of a real boson can cause not only a recoil of both fermions but a flip of their spins as well, as with, for example, photons.

Diagram 3 shows how an attractive effect between fermions with some or all opposed spins can occur via the exchange of virtual bosons. Note that the attractive effect arises mainly from a repulsive effect that works right around the hypersphere. The transactional mechanism in which advanced waves travel back from the future ensures the instantaneity of the effect.
Some further thoughts on the Hypersphere Quantology model: - The spinor vector representation can accommodate particle creation and annihilation by spins/antispins cancelling to energy or manifesting out of sufficient energy; and the transfer of spins between particles. Weak Force interactions involve electron/antineutrino, antielectron/neutrino, or electron/antielectron based bosons. Particle generation conservation still presents some problems – it seems globally conserved across entangled systems, but not locally conserved.
The Hypersphere Quantology model implies a more holistic view of the universe in which the wave/particle quanta which compose it ‘individually’ extend in some sense to everywhere within it and their properties depend on all the rest of it as in Mach’s Principle. Retroactive effects across transactional quantum handshakes implies indeterminate causal ordering and a fair dose of pure chaos in a universe where everything has a degree of instantaneous connection with everything else through the wave aspect of reality which approximates to what traditional magicians have called the Aether.
HYPERSPHERE QUANTOLOGY. - Nuclear Physics without Quarks.
Quantum Chromodynamics attempts to model observed nuclear phenomena in terms of six types of Quarks (and their corresponding antiquarks) which can combine in triplets to form Baryons such as the Proton and Neutron and in quark/antiquark pairs to form an extensive array of Mesons as real particles or virtual particle(field) effects.
However Quantum Chromodynamics remains a very baroque and messy model. Quarks require a description in which they have fractional nuclear and electromagnetic charges, they remain impossible to observe singly, they require eight different types of similarly impossible to observe Gluons to hold them together, and they also require clouds of unobservable virtual quarks to explain the observed masses and spins of the Baryons and Mesons that they combine to form. Whilst the Quark-Gluon-Colour model can describe fractional nuclear charges it does not really account for fractional electric charges or their absence in Leptons. Moreover, the observed properties of many Barons and Mesons require a description in terms of different types of quarks in peculiar superpositions of each other.
Hypersphere Quantology depends on the principles that the energy in particles consists of spacetime itself undergoing spinorial rotation in various dimensions and that sufficient energy always creates spin-antispin pairs which can mutually annihilate to energy again.

In the Hypersphere Quantology model, Barons such as the Proton and Neutron consist of quanta of spacetime which have three chiral spinorial rotations about their direction of propagation, one of which has the opposite chirality to the other two, summating to either spin + ½ or spin – ½ . They can also have extra spins which give rise to electric, nuclear, and generational ‘charges’. These extra spins lie in a spinorial relationship with all three of the ‘main’ propagation axes simultaneously.
Thus, the Hypersphere Quantology model does not use fractional electric or nuclear charges, nor does it require a suite of Gluons to hold Hadrons (Baryons & Mesons) together, nor does it require that seventeen different Fields permeate the whole of spacetime to explain quantum observations, only one Field exists – spacetime itself – which can carry spinorial rotations and subtend the resulting geometric twists in six dimensions.
The example diagram shows a variety of geometric twists that a Neutron can subtend as forward (retarded) waves and that a proton can subtend as backwards (advanced) waves. At low energies these retarded and advanced waves combine to create Field effects which we can denote as arising from Virtual Bosons if we wish to visualise their geometry in terms of particles, although they act in a far more ‘spread out’ fashion.
At higher interaction energies Real Bosons may form as discreet particles that can transfer momentum as well as force.
Mesons consist of unstable particle-antiparticle pairs. When Barons undergo very high energy interactions some of the energy can become sloughed off as fleeting pairs of positive and negative nuclear spins, and retarded and advanced waves of these can combine to form Mesonic fields of virtual particles, or at sufficiently high energies, Real Meson Bosons which tend to decay rapidly.
The spins which make up particles thus appear as more fundamental than the particles and fields themselves, and fields come into existence only between interacting particles. The retroactive nature of the advanced wave components guarantees that fields effectively have instantaneous effect and that Entanglement occurs.
Real Boson particles can come into existence if sufficient energy becomes available, and these appear to observation as quantised exchanges of momentum and spins (or charges) between emitter and absorber that propagate at lightspeed or less. Whilst ‘in flight’ such bosons travel as waves with positions and momenta that remain simultaneously unmeasurable and indeterminate.

So what implications does this Hypersphere Ontology hypothesis have?
It finally includes gravity in quantum theory, not so much by ‘quantising gravity’, but rather by ‘Geometricating the Quanta’.
It eliminates all the infinities that currently plague calculations in quantum physics. So-called Fundamental Particles do not consist of point particles of zero size, they consist of various spinorial rotation modes of the quanta of spacetime which subtend ‘twists’ that we observe as fields in the surrounding spacetime.
Because fields arise from a combination of retarded and advanced waves they effectively act instantaneously. The Sun attracts the Earth from its actual position in the sky, not from its apparent position about two of its own diameters behind that, from where the light left the Sun about eight minutes previously.
Real Bosons, like the photons of light, travel at lightspeed, as do real Graviton bosons (the so-called gravitational waves). Fields act to instantly ‘feel out’ what lies in spacetime, and then if sufficient energy becomes available, a disturbance can propagate through that field at lightspeed.
Fields and the movements of real bosons thus ensures some degree of Quantum Entanglement between all the apparent particles and structures in the universe.

All particles extend fields right around the hypersphere of the universe, these converge at antiparticles at their antipodes. This explains the apparent lack of antimatter in the universe.
In/Out waves of spin converge and undergo 3-rotation to make non-point particles of finite size.
Every particle depends for its properties on the whole of the rest of the universe.
The Ubiquity Constant and the quantisation scale depend somehow on the macrostructure of the universe.
Quantised ‘kinks’ in space can only move at lightspeed, or less if they embody the temporal electric or nuclear spins which confer mass.
The Higgs mechanism does not apply. If the tiny 125 GeV blip corresponds to anything it probably corresponds to a transient ZZ di-boson.
Volume = 2pi2r3 for both a hypersphere and a (Clifford?) horn torus.
Does the local field geometry change from a vorticitating 3-Hypersphere to two rotating 3-Tori upon particle-antiparticle pair production and thus confer particle directionality?
Can Macrostructures modulate waves to carry structural information?
If so, all manner of psi effects and morphic field effects become possible and the universe will exhibit Stochastic Holism.
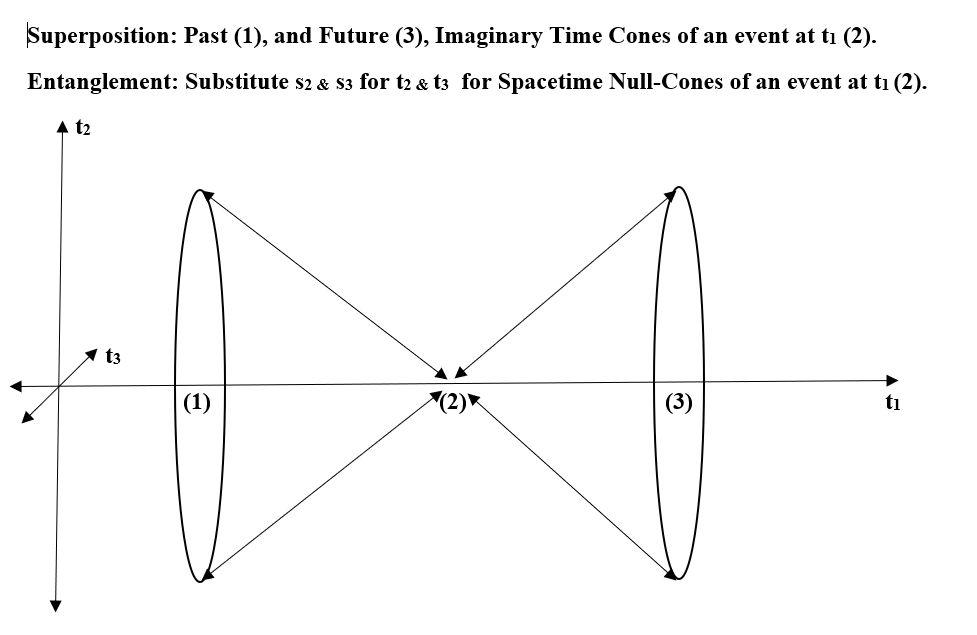
Three Dimensional Time Resources.
Herewith a selection of some of the main papers on 3D Time and SO(3,3) spacetime.
https://arxiv.org/pdf/quant-ph/0510010.pdf
https://phys.org/news/2007-04-mathematician-extra-dimensions-time-like.html
See also original paper, later published by the Royal Society.
https://arxiv.org/pdf/gr-qc/0610068.pdf
https://www.researchgate.net/publication/278410426_Could_time_be_three-dimensional
https://arxiv.org/pdf/quant-ph/0510010.pdf
http://cdsweb.cern.ch/record/688763/files/ext-2003-090.pdf
Herewith a fascinating piece of speculation from Gerard 't Hooft
https://arxiv.org/abs/2107.14191
https://arxiv.org/pdf/2107.14191.pdf
See the 'fast variables' and multidimensional toroids.